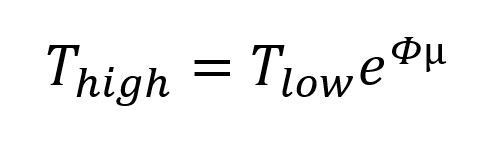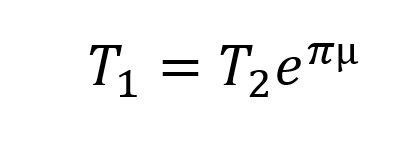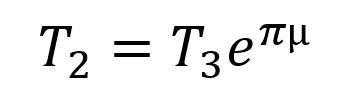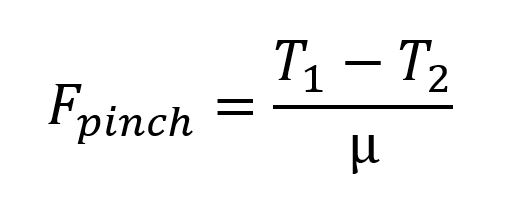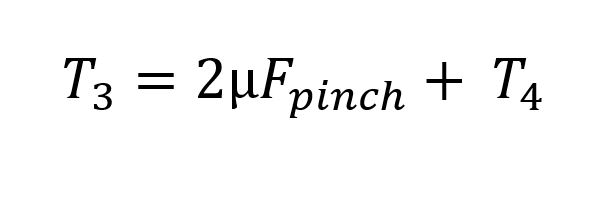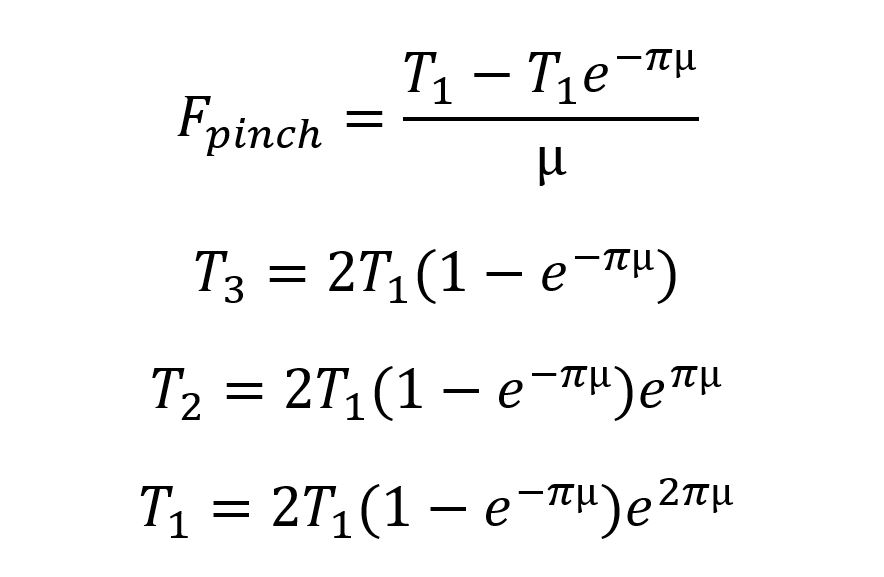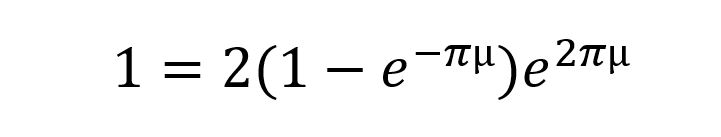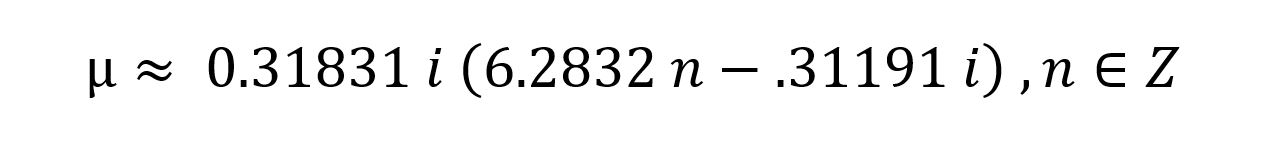If you described my lifestyle lately as “Doing math and playing outside,” I could hardly criticize you. Like many other engineers at Simplexity, I spend a fair amount of time outdoors. This year I’ve been hiking a lot, climbing some mountains and some rocks, and training for my first ever marathon. Between the weekends I spend my days at Simplexity doing mechanical analyses like force and strength analysis, CAD, spring design, tolerance stacks, stability analysis. Nerdy stuff to be sure, but I love it. These are two of my obsessions. And sometimes I like to bring them together.
On the outdoor side of things, I’ve gotten really into slacklining. Slacklining is, at its core, about the same as tight-rope walking. The line is looser (1 to 6 kilo newtons opposed to 80 for tight ropes) though still typically taught, and it’s made out of flat webbing instead of round rope or cable. Different slackline disciplines do different things, some high in the air (high-lining), some over water (water-lining), some especially long lines (long-lining), some saggy lines swinging back and forth (rodeo) and some emphasize tricks (trick-lining).
For me, it’s been short lines close to the ground. Progress was quick, and I was walking within the first month. For me though, I can engage with my slacklining better by mixing in some engineering. I’d like to share some engineering and slack-math.

An engineering challenge faced by the early slack-liners (in the 1980’s and 1990’s) was how to attach the webbing. Those pioneers often just tied the webbing with a clove hitch knot to a carabiner or shackle. But webbing hates knots. Knots cause stress concentrations, some fibers hold more tension than others in the area of the knot. In this way knots leave the webbing with only perhaps 30% of its strength. A better solution was required, and someone invented it. It’s a mechanical device called a weblock. They’re available from numerous manufacturers.

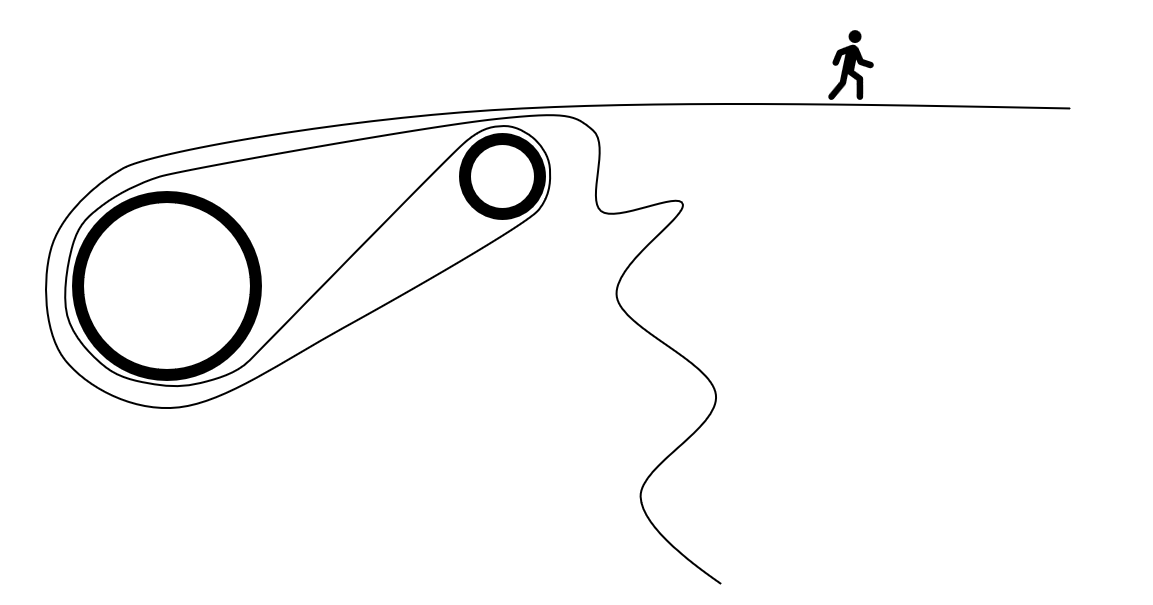
The weblock consists of two metal plates with a large round drum and a removable pin between them. The two plates also feature a hole or holes in the back which allow it to be attached to the anchor. Every one of the weblocks has a little diagram on it which shows you how to run the webbing around the “diverter” drum and pin. The diagrams usually look like this:
My Rendition of the common weblock diagram
I guess there’s a law somewhere that they have to have the little man walking on the line in the diagram. When I see that diagram, it’s as if they’ve already laid out the analysis for me. See? We’re basically done!
Did you see the analysis all laid out the way I did?
So, this device operates using friction. And at some amount of friction, the webbing will slip through the device. Figuring it out was a fun bit of analysis. Let me share!
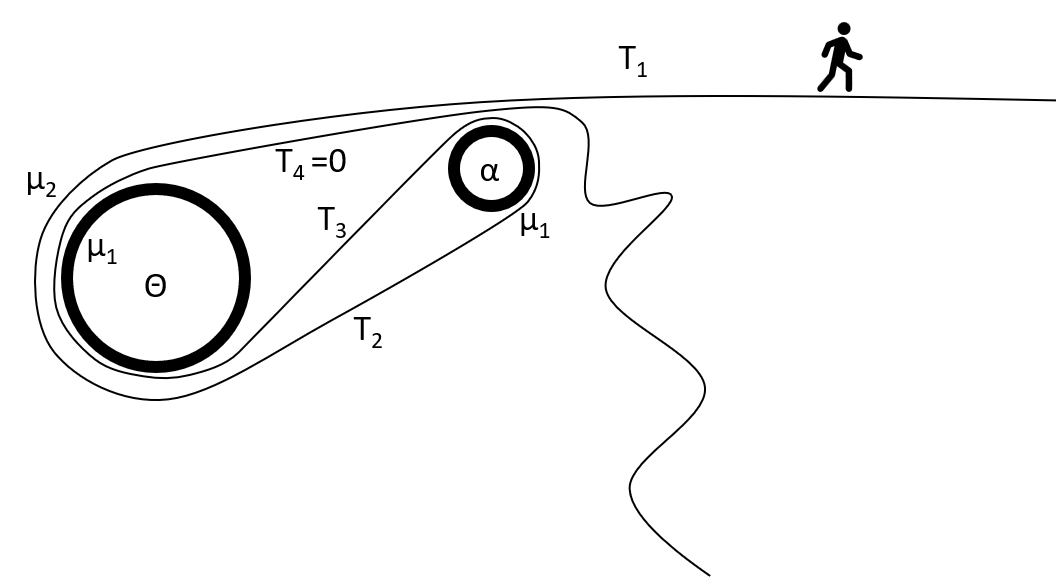
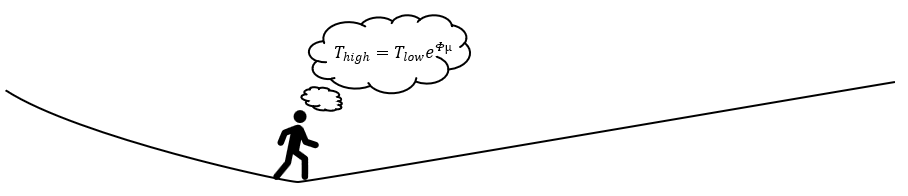
The first thing you need to know to analyze weblocks is the capstan equation. Basically, if a rope is sliding while wrapped around a drum, and there’s friction on the drum, the tension in the two sides of the rope will be at a fixed ratio:
T’s are tensions, φ is the wrap angle around the pole (radians) and µ is coefficient of friction. I like that equation. When I’m doing math for fun, I like to make simplifying assumptions. When it’s for work, though, I’ll pull the simplifications out later. To simplify, let’s assume that both wrap angles are about π (180°) and that the friction is the same for both were webbing rubs on the metal or itself µ1=µ2=µ. At what µ does the webbing slip?
Well let’s just start applying the capstan equation:
And then also:
So far, it’s easy… but now the webbing wraps back under itself, so things get a little more complex. Because the webbing between T3 and T4 is pinched by the webbing above. So, we just have to figure out how much pinch force there is on that piece of webbing.
That pinch force will be the friction of the outer webbing, divided by the coefficient of friction.
So, the friction experienced on the inner piece of webbing will be coefficient of friction times the pinch force times two because there’s friction on both sides.
And T4 is 0. I see that coefficient of friction about to cancel out! So, let’s solve for T1; it looks like we can. I’ll skip some steps because I’m lazy with the equation editor.
This is the part in the math where I see that T1 start to fall out and I get nervous. So, I ask myself, “what am I trying to accomplish?” Well, I’m trying to figure out when the weblock slips. So, for the weblock to slip, these equations have to be true. At what friction µ are these equations true?
Ok, I’m sure there’s a lot of simplification I could do here and some clever math to work this out. But with the ghosts of a dozen math teachers standing over my shoulder and shaking their heads at me, I’ll just type this into a symbolic solver online…and I get this nasty thing:
So uhhh, what’s going on? Well there are a bunch of imaginary solutions, which in this case we don’t care about….and one real solution: µ=0.099. So, for values of friction below that, things start accelerating and make my equations above untrue. And for values above 0.099, nothing slips. My equations are untrue if nothing slips because a fundamental assumption of the capstan equation is that the rope is slipping.
I think this is an interesting value because it’s low for unlubricated friction but not that low. With most plastics giving friction between 0.15 and 0.25, it doesn’t give much margin of safety. That lack of margin of safety explains several things manufacturers tell users about weblocks. First, they always recommend one of several methods of tying off the loose webbing tail. Second, they caution users about micro-slipping, where if the line is bounced or vibrated in the right way, the webbing will slip through weblocks bit by bit. Vibration frequently has the effect of reducing friction. Also, manufacturers caution users about some types of webbings made out of particularly slippery materials like Dyneema or Spectra. These webbings don’t hold in weblocks without special wrapping techniques.
So, having done a little math, I now know what holds me up on my slackline! I’m going to go out and do a little rope walking now!
Video of me slacklining
Me, walking a line, doing math